Introdução

Em programação é comum vermos o termo Sign Extension quando trabalhamos com código mais baixo nível, e muitas pessoas acabam não entendendo de fato o que acontece quando ocorre a extensão de sinal.

Para entender a extensão de sinal é necessário entender como o complemento de 2 funciona, que é a forma como as cpus codificam números negativos em binário.

Estude isso

Complemento de 2 é muito importante em programação, então estude sobre o assunto!

Vou começar então dando uma revisada bem rápida sobre complemento de 2

Revisão sobre Complemento de 2

Aqui no canal eu já fiz um vídeo explicando com mais detalhes o que é complemento de 2. Acesso pelo link abaixo se quiser ver mais a fundo.

//link

Quando trabalhamos com números sem sinal (unsigned) os bits de uma variável numérica representam o próprio número, começando de 0 e indo até a valor máximo dependendo do tamanho em bits da variável. Nenhum segredo aqui.

O problema surge quando queremos representar números negativos. Como no fundo tudo são bits, como representar um número negativo?

Temos então que dividir as variáveis númericas em 2 tipos, as unsigned (sem sinal) e as signed (com sinal). As unsigned é o que já falamos acima e não tem segredo, porém e as signed?

Uma variável com sinal pode ter números negativos e positivos, então como a cpu representa um número negativo?

Números negativos

Em variáveis com sinal, o bit mais significativo representa o sinal. O bit 0 indica positivo e o bit 1 indica negativo.

É isso, definimos o bit mais significativo como sendo o sinal do número, conforme imagem abaixo:

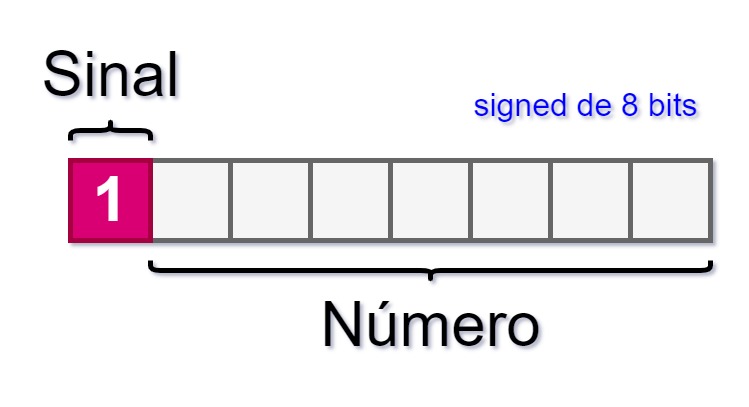
Então esse bit dentro da variável passa ter uma outra função, que é indicar o sinal.

Ok, fazer só isso trás alguns problemas, como termos dois zeros agora, como mostra a figura abaixo:

Isso é um problema. Outro problema é que as contas, como adição, passam a ficar esquisitas e sem lógica, como mostra a imagem abaixo:

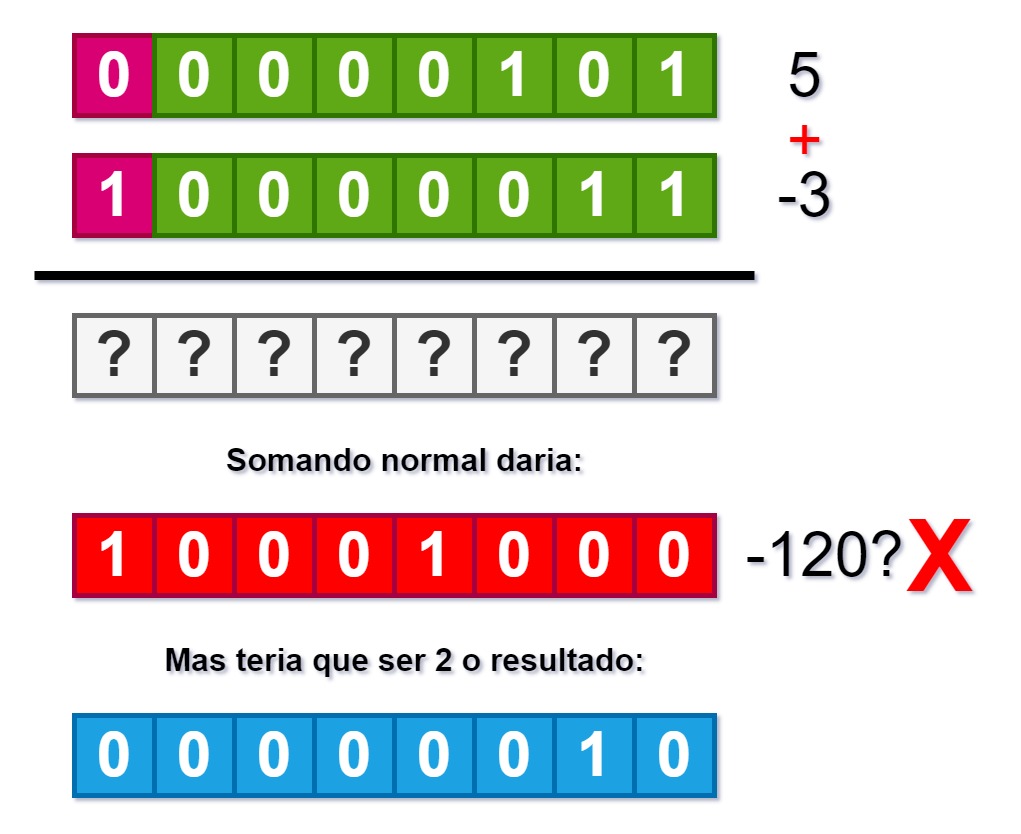
Lembre que na matemática as duas linhas abaixo são equivalentes:

// 5-3 // 5+(-3)

Em matemática podemos somar um número positivo com um negativo e faz sentido, então seria interessante conseguir isso em binário tb. Porém com a solução atual não tem como. E fica o problema dos dois zero ainda.

A solução é o complemento de 2, que fica mais fácil ser explicado com o método do odômetro. O odômetro é o marcador de kilometragem de um carro ou moto.

Imagine um carro zero kilômetro, onde o odômetro está marcando 0000 (vou colocar 4 digitos aqui pra simplificar). Ao andarmos com o carro a kilometragem vai subindo, 0001, 0002, 0003, e assim por diante.

Agora imagine que andamos de marcha ré com o carro e a kilometragem vai diminuindo. A figura abaixo mostra o que acontece.

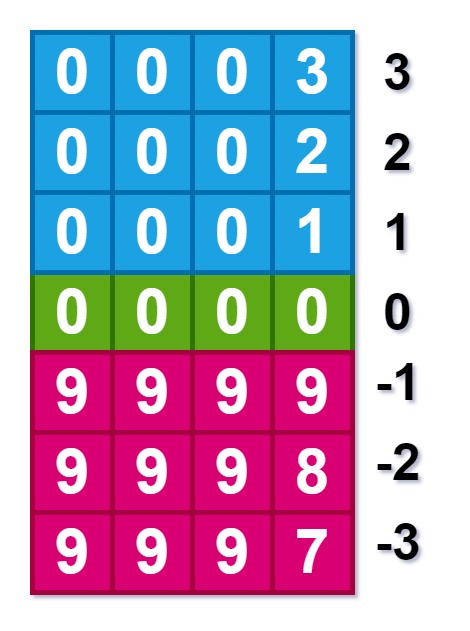
Se estivermos com o marcador em 0000, se andarmos 1km de marchá ré o marcador vai pra 9999, certo? Depois vai diminuindo quanto mais andarmos de marcha ré.

No caso poderíamos considerar o -1 como se fosse o 9999 do odômetro, pois o 9999 é 1km pra trás. Faz sentido?

O mesmo pode ser feitos com bits, como mostrado na imagem abaixo:

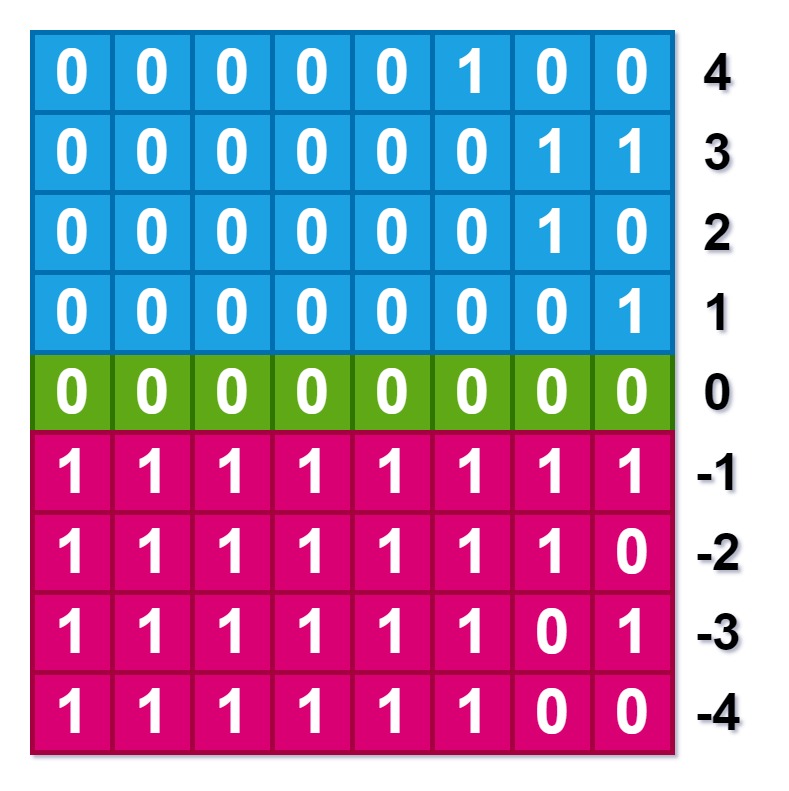
Se estamos com o valor 0x00, se andarmos 1 bit pra trás voltamos pra 0xff.

Portanto o 0xff é o -1 em complemento de 2. Em 16 bits o -1 seria 0xffff. Em 32 bits seria 0xffffffff, e assim por diante.

Mas isso funciona?

Funciona! O bit mais significativo ainda pode ser usado pra indicar se é positivo ou negativo.

Como o bit mais significativo ainda pode ser usado pra ver o sinal, se começarmos a decrementar o valor a partir de 0xff (considerando 8 bits), vemos que o menor valor que teria o bit mais significativo com 1 seria o 0x80, pois se subtraírmos mais 1 ficaria 0x7f, que já tem bit mais significativo como 0.

A imagem abaixo mostra o range de valores para uma variável com sinal de 8 bits e os bits correspondentes.

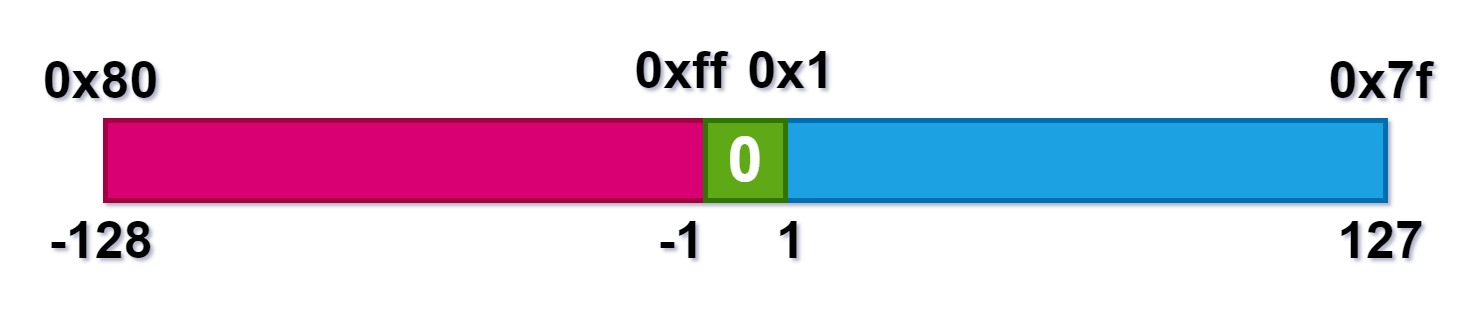
Vemos então que o menor valor é o -128, que corresponde ao hexa 0x80 e o maior valor é o +127, que corresponde ao hexa 0x7f. Se fosse 16 bits o menor valor seria 0x8000 e o maior 0x7fff, e assim por diante.

Com o complemento de 2 todos os problemas são solucionados, incluindo a aritmética. Se somarmos um número positivo com um negativo em complemento de 2, o resultado é o esperado, como mostrado abaixo aomando 5 com -3:

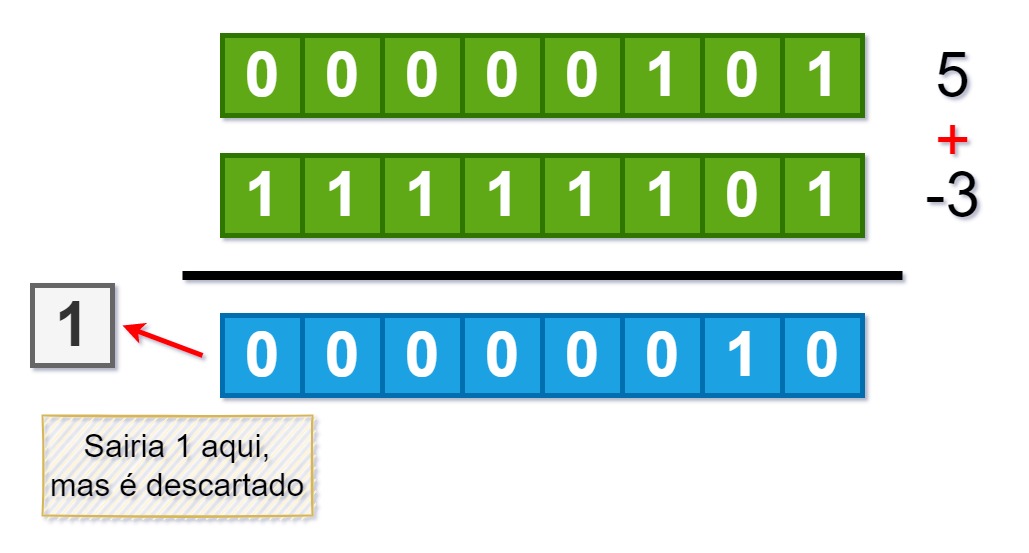
Por que tem esse nome?

Se invertermos todos os bits de uma variável (0->1 e 1->0), isso é chamado de Complemento de 1. Se somarmos 1 no complemento de 1 teremos o Complemento de 2, que possui a característica do odômetro que foi explicado. Com o médoto do odômetro fica bem mais simples de entender, não é mesmo?

Extensão de Sinal

Ok, sabemos que os números negativos são representados como complemento de 2 pelas cpus, então o que é extensão de sinal?

Extensão de sinal aparece quando temos uma variável de um certo tamanho e desejamos aumentar o número de bits desta variável mantendo o mesmo valor no final. Por exemplo se tivermos uma variável de 8 bits e queremos aumentar pra 16 bits ou 32 bits, mantendo o mesmo número.

Como exemplo se tivermos uma variável de 8 bits com o valor 7, se aumentarmo pra 16 bits queremos que o valor continue 7. Se o valor fosse -5 queremos que continue como -5 quando aumentamos o número de bits da variável. Simples assim.

Quando ocorre?

Extensão de sinal ocorre quando temos um dado numérico e desejamos expandir o número de bits deste dado, fazendo com que o número fique com o mesmo valor.

O detalhe principal ocorre quando temos números negativos, que é o principal a se entender.

Mas antes, vamos falar primeiro das variáveis unsigned, sem sinal.

Variáveis unsigned.

Imagine que temos uma variável unsigned de 8 bits com o valor 7 e queremos expandir pra 16 bits, como na imagem abaixo:

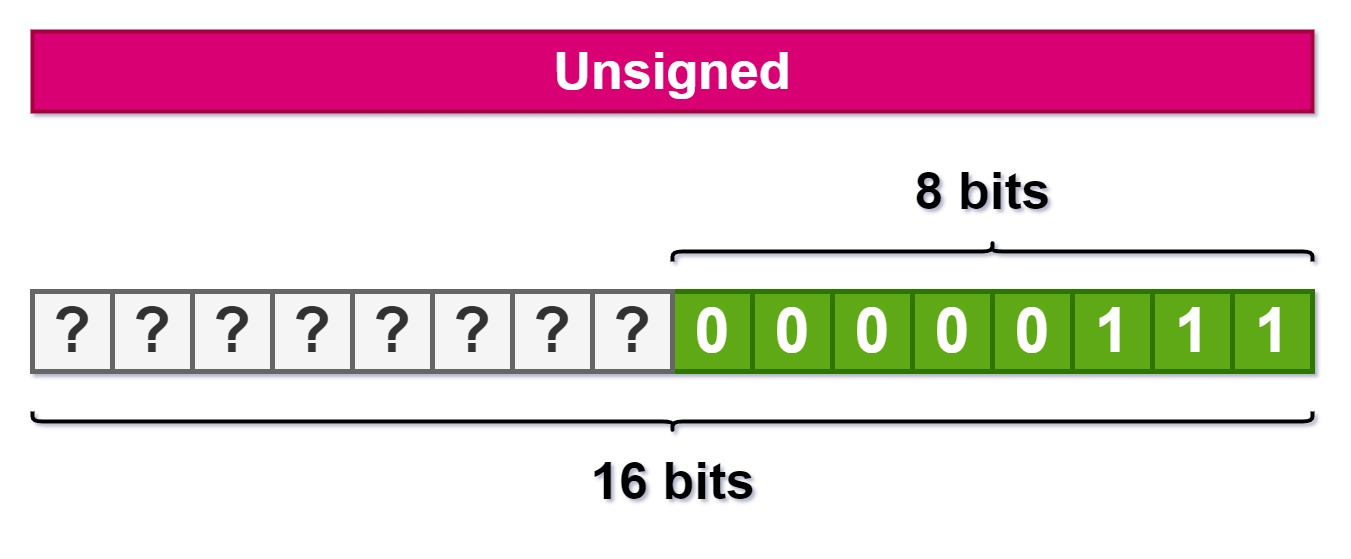
O que temos que colocar no novo byte da esquerda?

Temos que colocar 0x00, certo? Pois assim a valor final fica 0x0007 e assim continua com o mesmo valor 7, como na imagem abaixo:

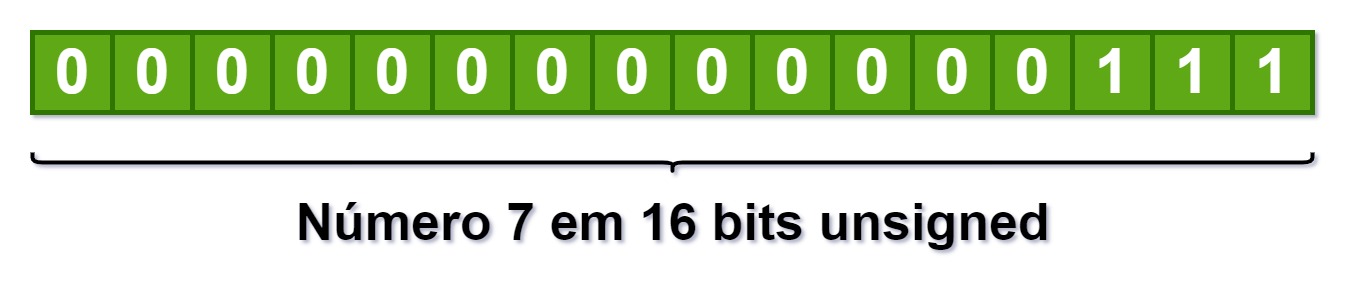
Então pra unsigned não tem muito segredo, pois sempre temos que colocar 0x00 nos novos bytes, uma vez que pra unsigned o menor número é o 0, então colocando zeros na esquerda o número continua o mesmo.

Variáveis signed (com sinal)

Aqui que entra a extensão de sinal.

Imagina que temos uma variável signed de 8 bits com o número 5 e queremos aumentar o tamanho da variável pra 16 bits mantendo o valor. O que temos que colocar no byte da esquerda na imagem abaixo?

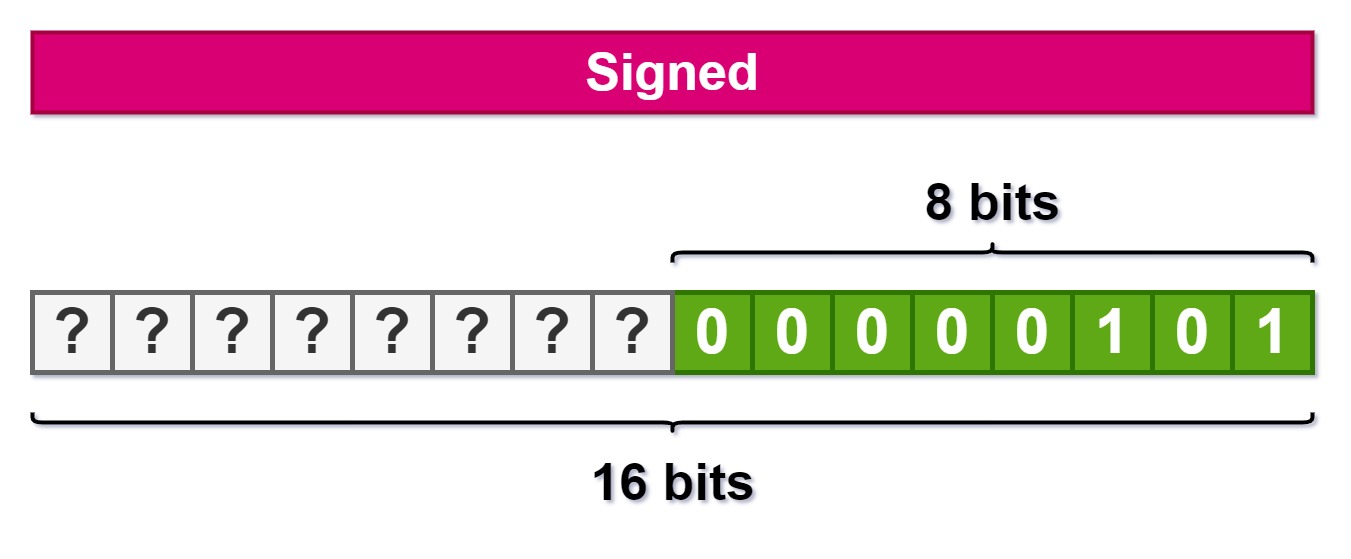
Temos que colocar 0x00, certo? Pois aí o valor final fica 0x0005, que continua 5. Veja a imagem abaixo:

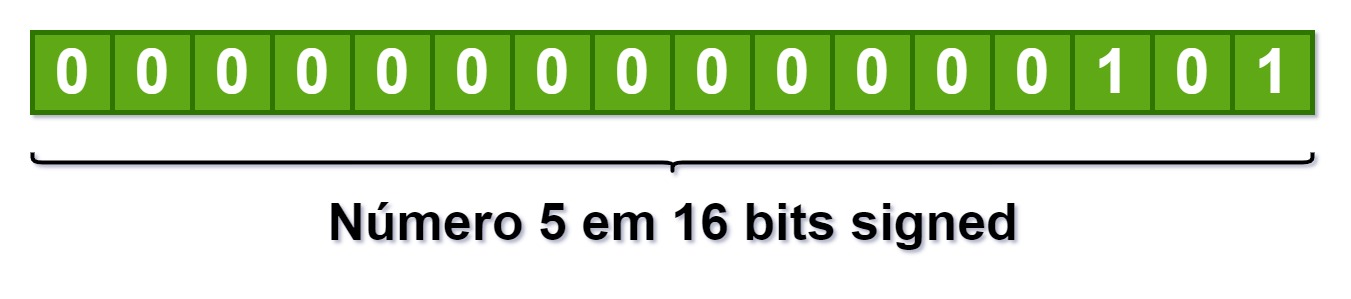
Aparentemente nada mudou em relação ao unsigned.

Mas agora se tivermos uma variável signed de 8 bits com o valor -3, que é 0xfd em complemento de 2 e queremos aumentar pra 16 bits mantendo o número final como -3, o que devemos colocar no byte da esquerda da imagem abaixo?

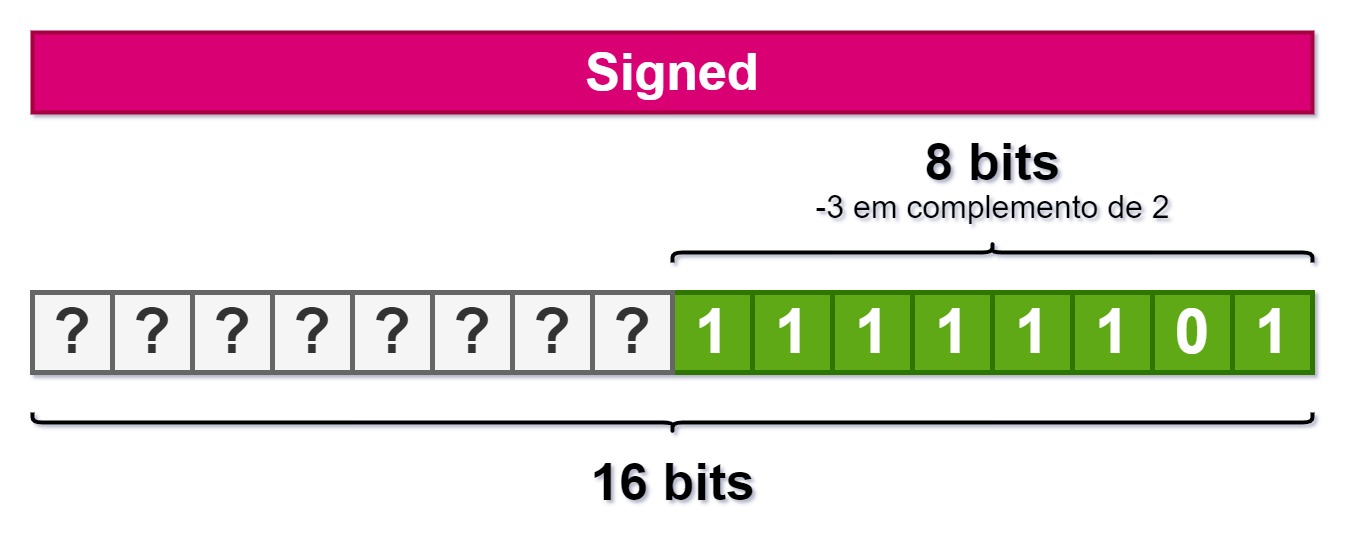
Se falou 0x00 errou feio. Se colocar 0x00 o número final vai ficar *0x00fd, que em 16 bits equivale a 253, ou seja, nada a ver com a resposta.

Então como que seria -3 em 16 bits em complemento de 2? Seria 0xfffd, certo? Então a resposta seria colocar 0xff no byte da esquerda da imagem acima.

Então para números com sinal tem casos que precisamos colocar 0x00 e outros casos que precisamos colocar 0xff.

Qual a regra pra isso?

A regra é expandir o bit de sinal da variável que você deseja aumentar, copiando o valor do bit de sinal, que é 0 ou 1, para todos os bits novos que adicionar.

Então para variáveis com sinal temos que pegar 0 bit de sinal da variável atual, seja 0 ou 1, e copiar para todos os bits novos que forem adicionados.

A imagem abaixo mostra como fica para o caso do número 0x5:

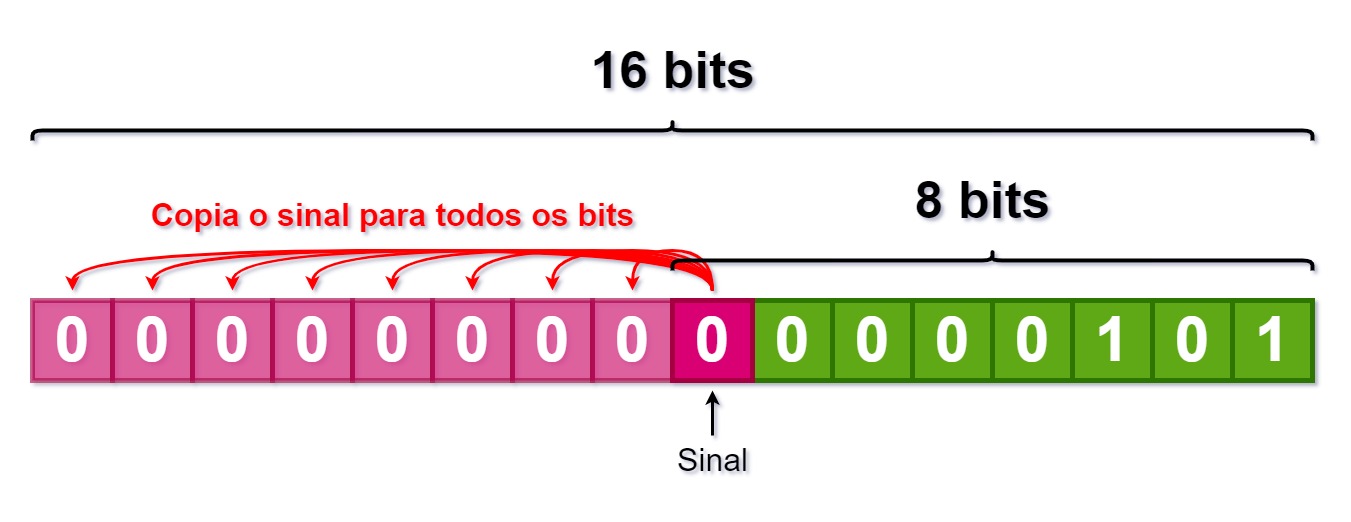
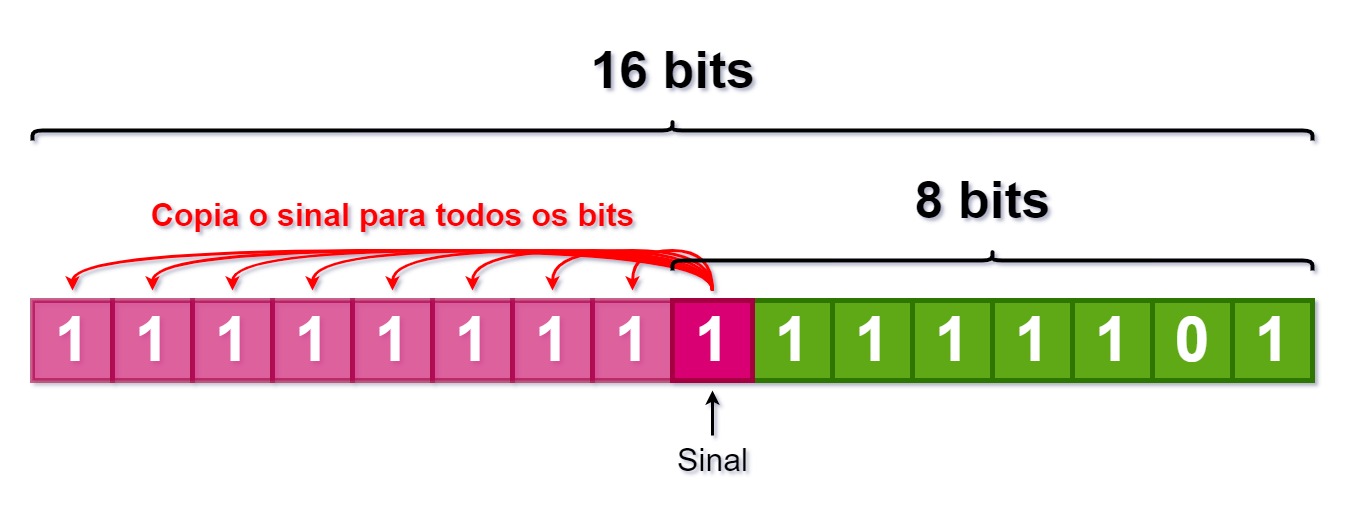
A imagem abaixo mostra como fica para o caso do -3, que é 0xfd em complemento de 2.

Quando acontece extensão de sinal no dia a dia?

Em linguagens como C/C++, se tivermos uma variável signed, tipo um char, short ou int e fizermos um cast para uma variável com tamanho maior, ocorrerá extensão de sinal. Isso acaba passando despercebido muitas vezes pois nessas linguagens trabalhamos com os números na forma matemática no meio do código, como -3, -1000, etc, e não com a representação hexadecimal do complemento de 2. Mas se printarmos em formato hexadecimal (com %x em C/C++) um int que possui o valor -3, veremos que o valor 0xfffffffd, porém um print normal (com %d) retornaria -3.

Linguagens de alto nível

Em linguagens de alto nível você encontra diretamente os efeitos da extensão de sinal se estiver trabalhando em algum momento com o formato hexadecimal ou binário de uma variável. Se surgir um monte de 0xff do nada você já sabe o que é.

Extensão de sinal no Snes e Mega Drive

Nos Snes e Mega algumas instruções fazem extensão de sinal em alguns casos, principalmente no Mega Drive onde o 68000 trabalha com até 3 tamanhos de dados, .b, .w e .l. Veremos esses casos quando aparecerem, porém agora já sabemos o que é a extensão de sinal.

Instrução EXT no 68000

Pra finalizar vou falar da instrução ext do 68000 do Mega Drive que serve para fazer a extensão de sinal de um registrador de dados. Temos esses 3 casos:

ext.w d0 //expande o d0 de byte pra word
ext.l d0 //expande o d0 de word pra long
ext d0   //equivale ao .w

Instrução ext

Faz extensão de sinal de um registrador de dados de acordo com o tamanho passado. Se for .w faz extensão de byte pra word, copiando o bit 7 para os próximos 8 bits. Se for .l faz extensão de word pra long, copiando o bit 15 para os próximos 16 bits. O 68000 não faz extensão direto de byte pra long.

A figura abaixo mostra o que a instrução ext faz:

Como dá pra ver não existe forma de expander de byte pra long direto. Para isso temos que usar as duas formas em sequência, expandindo de byte pra word e depois de word pra long. Versões posteriores da família do 68000 adicionaram uma instrução extb que faz a extensão de byte pra long, porém ela não existe no 68000 usado no Mega Drive.

E no Snes?

A cpu do Snes não tem uma instrução dedicada pra extensão de sinal. Mesmo pq a cpu do Snes tem acumulador de 8 ou 16 bits, então não faz muito sentido.

Código de exemplo

O código que rodei no vídeo está abaixo para referência.

move.l #$80,d0

ext.w d0
ext.l d0

move.l #$12345678,d0
ext d0

move.l #$fedcba98,d0
ext.l d0