Introdução

Neste episódio vou explicar o que é overflow em programação, tanto com sinal (signed), como sem sinal (unsigned).

Overflow é algo meio chatinho pra quem não está acostumado com esses detalhes mais baixo nível, pois sempre aparece em textos de programação mas muita gente não sabe o que significa de verdade.

A forma como o overflow ocorre varia de operação para operação, como soma, subtração, shift, etc. Neste episódio vou focar na soma, pois ela ilustra bem o que é e como ocorre o overflow. No final vou dar uma explicação de como ocorre o overflow na subtração e shift.

Pré-requisitos

Para entender este assunto você tem que entender sobre números binários, hexadecimais, complemento de 2 e soma e subtração binária. Eu tenho vídeos sobre todos esses temas aqui no canal.

Signed (Com Sinal) e Unsigned (Sem Sinal)

A primeira coisa a entender é que um registrador tem um certo tamanho em bits, no caso 32 bits para o Mega Drive e 16 bits para o Snes. Com esses números podemos representar números com sinal e sem sinal. Isso fica a cargo do programador, pois bits são bits. Então as Cpus geralmente tem instruções e flags para tratar os dois casos.

Então podemos por exemplo colocar um número de 32 bits em um registrador do Mega Drive e considerar que é unsigned. Em outro momento podemos colocar um número de 32 bits em um registrador e tratar como signed, onde neste caso os números negativos estariam em complemento de 2.

Mas como a Cpu sabe quando um número é com sinal ou sem sinal? A resposta é que ela não sabe se um número em um registrador é um número com sinal ou sem sinal. O que fazemos com os registradores, as instruções que usamos e as flags da Cpu é que vão dar sentido a essas questões.

Por exemplo, se fizermos uma soma de dois registradores, a Cpu vai fazer a soma binária da forma usual, sem levar em conta essas questões de sinal. Porém as flags n (negativo) e v (overflow) vão ser alterada levando em conta o fato de que os números sejam com sinal. Porém se para o programador os números eram sem sinal, ele não vai levar em conta essas duas flags na sequência do código, pois essas duas flags só fazem sentido para contas com sinal.

No final das contas a soma é igual para ambos os casos com sinal e sem sinal, então cabe ao programador usar as flags que fazem sentido para a ocasião.

A partir desses detalhes dos sinais, podemos entrar na explicação de Overflow.

O que é Overflow?

Overflow ocorre em alguns tipos de operações, como soma, subtração, shift, etc, e está relacionado com a troca do sinal do resultado em comparação com os operandos. Calma que vou explicar com exemplos.

Várias tipos de instruções geram overflow e os detalhes variam, então aqui vou focar apenas na soma, e futuramente quando vermos alguma outra instrução que gera overflow eu explico os detalhes, porém tudo gira em torno do que vou explicar aqui para a soma.

Para a soma ocorre o overflow quando somamos dois números com o mesmo sinal e o resultado tem um sinal diferente. Por exemplo, se somarmos dois números positivos e o resultado for negativo, isso é um overflow, pois a soma de dois números positivos tem que ser positivo porém o resultado final no registrador ficou negativo (o bit mais significativo com 1).

Considere a soma dos números 0x3000 com 0x6000, como por exemplo nas instruções abaixo:

  move.w #$3000,d0
  addi.w #$6000,d0

O resultado é 0x9000, e quando estamos tratando os registradores como unsigned esse valor é correto e não há problema nenhum.

Porém a flag V da Status Register é setada pois se tratarmos os valores nos registradores como número com sinal, ocorre Overflow, uma vez que em ambos os números o bit mais significativo é 0, porém no resultado o bit mais significativo é 1, o que indica um número negativo. A figura abaixo mostra isso:

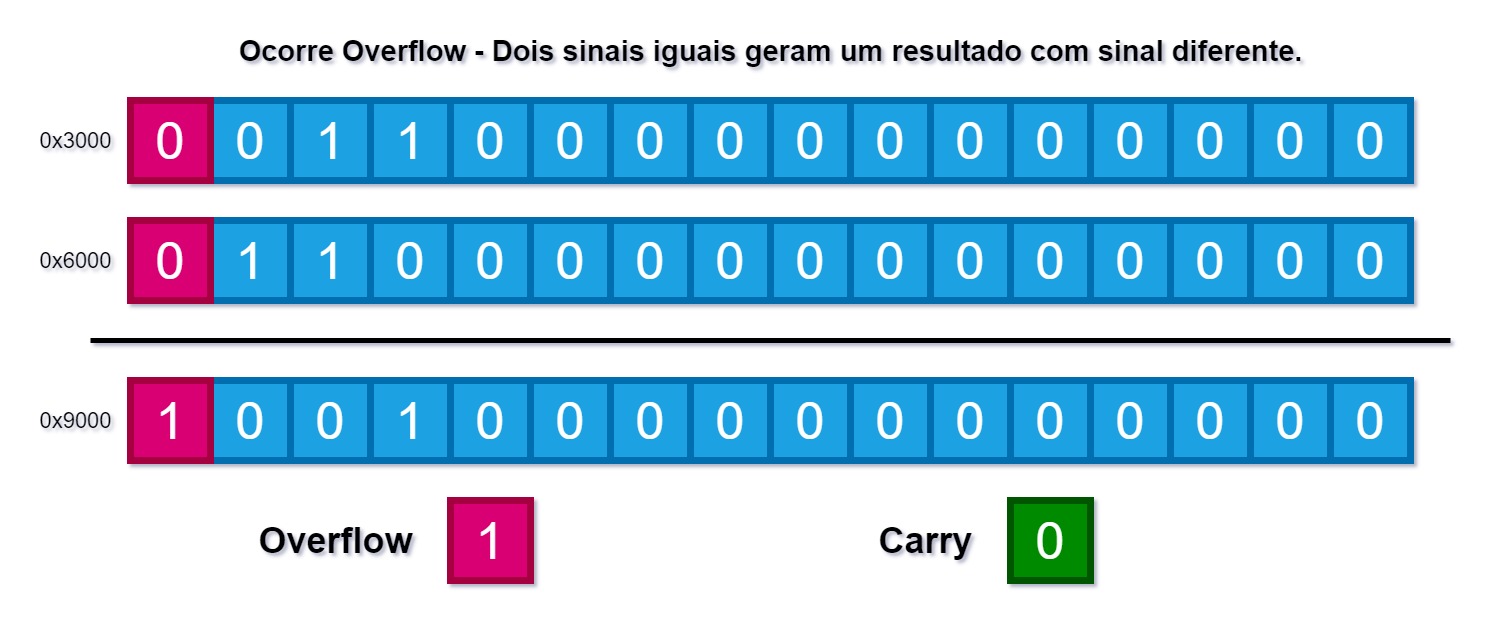
Então se considerarmos os números como signed, a soma não cabe no range dos números positivos, que vai de 0x0000 a 0x7fff, então isso é um overflow. Mas se tratarmos os números como unsigned, a flag v não deve ser considerada, então o resultado é o esperado.

No caso acima apesar da soma não “caber” no range de 0x0000 a 0x7fff, a carry flag não é setada pra 1 pois a carry só vai pra 1 quando a soma unsigned não cabe no registrador como um todo. Então é a flag v que indica esse “estouro” quando é signed. Tem como ambas as flags c e v irem pra 1, como veremos mais abaixo nos exemplos.

Novamente, as flags n e v são apenas para números com sinal. As outras flags, como c, z, etc, servem para ambos os tipos.

Agora vejamos a soma abaixo:

  move.w #$d000,d0
  addi.w #$6000,d0

A soma de 0xd000 com 0x6000 dá 0x3000. A carry c é setada para ambos os tipos signed e unsigned.

Porém a flag v fica com 0 neste caso, ou seja, não tem overflow, pois os números tem sinais diferentes se considerarmos eles como signed.

Portanto quando os dois operandos não tiverem o mesmo sinal nunca ocorre overflow. Só existe overflow se os dois operandos tiverem o mesmo sinal.

A figura abaixo ilustra esse caso:

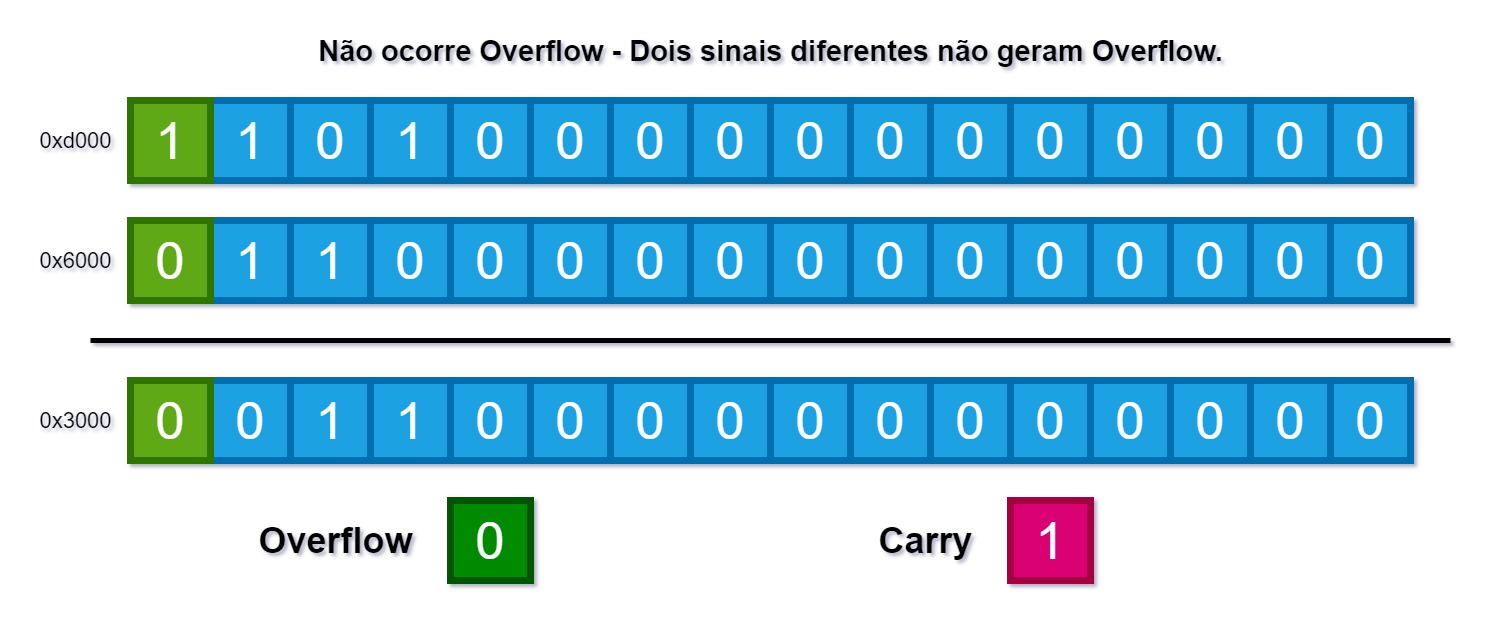
No próximo exemplo temos esse código:

  move.w #$a000,d0
  addi.w #$b000,d0

A soma de 0xa000 com 0xb000 dá 0x5000, então neste caso ocorre overflow pois os dois operandos tem o mesmo sinal e o resultado tem um sinal diferente, como mostra a imagem abaixo:

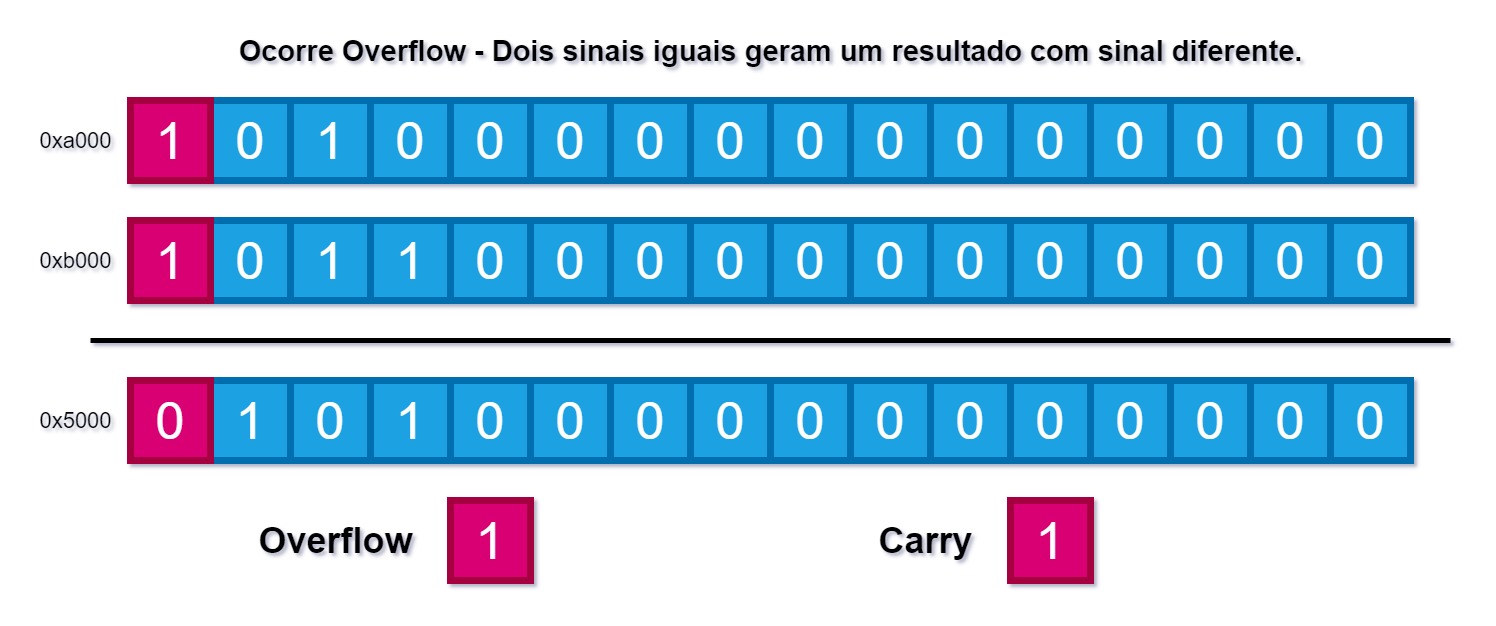
Como um último exemplo, considere o código abaixo:

  move.w #$d000,d0
  addi.w #$e000,d0

A soma de 0xd000 com 0xe000 dá 0xb000, então nesse caso não tem overflow pois ambos os números são negativos e o resultado é negativo.

A imagem abaixo mostra esse exemplo:

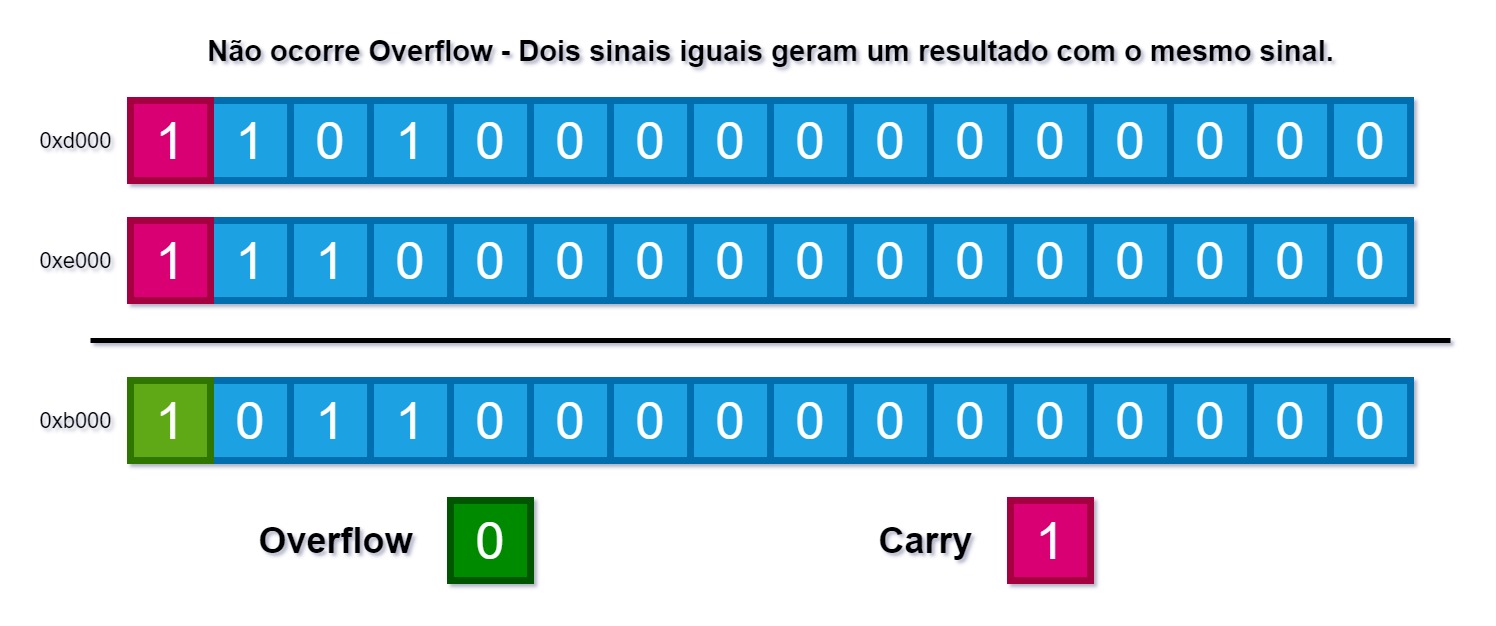
Exemplos para Unsigned

Nos quatro exemplos anteriores, se considerarmos todos os números como unsigned as contas funcionam como uma soma normal e só estamos interessados na flag carry c pra saber quando a soma estourou o limite do registrador. Esse “estouro” também é um tipo de overflow, porém nas Cpus um overflow tem a ver apenas quando tratamos os números como signed.

Então no caso do unsigned a imagem abaixo resume todos os exemplos anteriores:

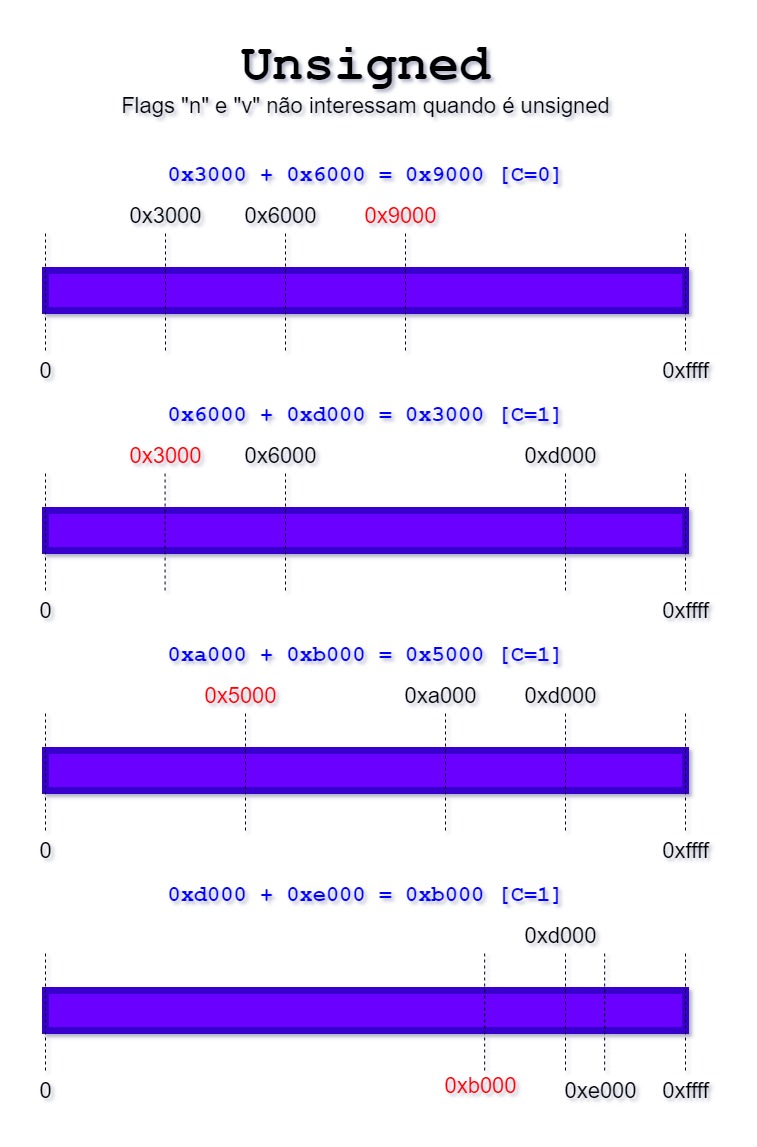
Na imagem consideramos os números positivos com a cor roxa, e como todos os números são positivos quando os tratamos como unsigned, o range total vai de 0x0000 a 0xffff.

Exemplos para Signed

Se considerarmos os números dos 4 exemplos anteriores como signed, então as flags de negativo n e overflow v precisam ser consideradas, além da carry c

A diferença aqui é que temos agora números positivos e negativos, e os negativos estão em formato complemento de 2. Então a figura abaixo resume os quatro exemplos anteriores, com os números positivos em roxo e os negativos em rosa:

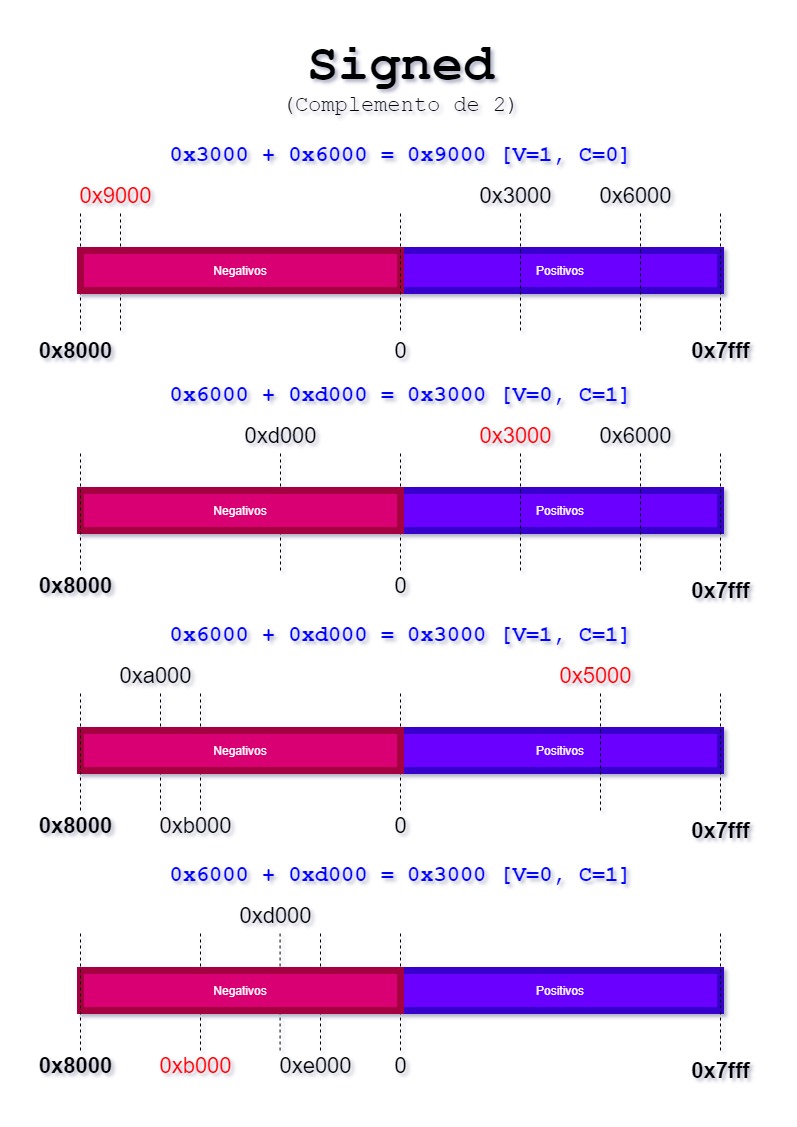
Notem que com complemento de 2 o 0 fica melhor representado no meio, com os positivos indo de 0x0000 a 0x7fff na direita e os negativos indo de 0x0000 a 0x8000 na esquerda.

Como a Cpu calcula o Overflow?

A partir do que foi explicado acima, a Cpu utiliza um método para verificar se um overflow pode ocorrer ou não, que é comparar o bit que vai para a carry com o bit que entra no MSB (o bit mais significativo). A figura abaixo mostra os 5 casos possíveis.

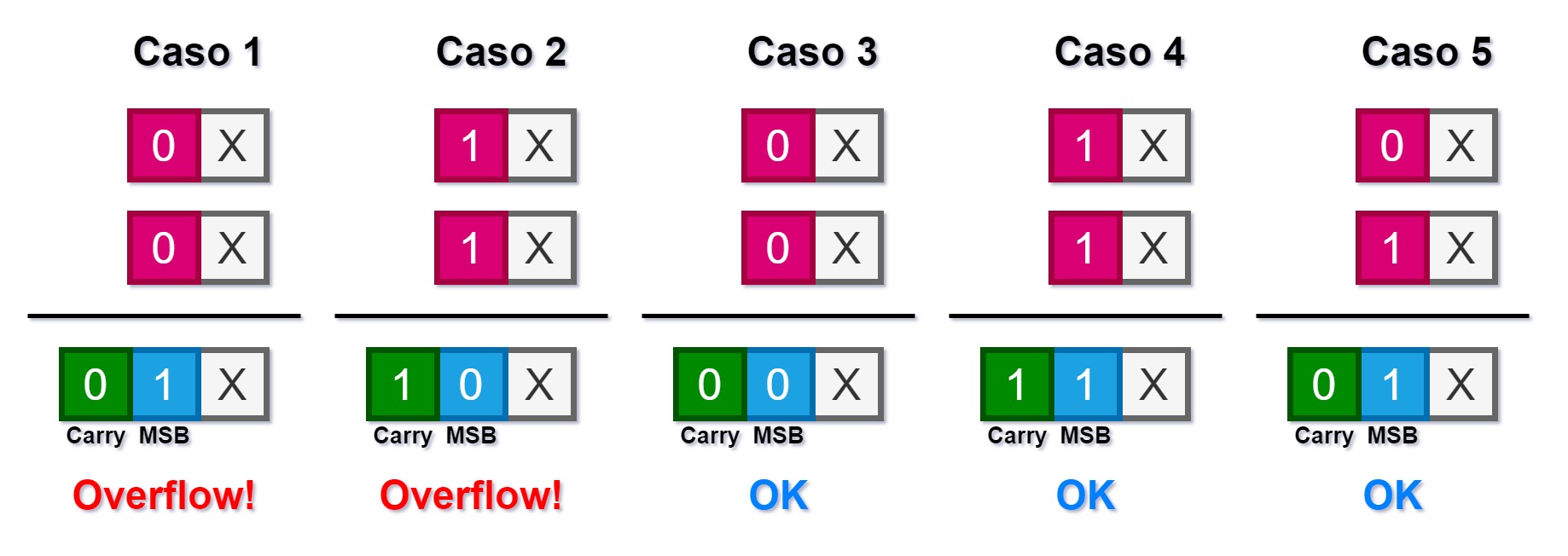
Na figura acima o X representa o restante dos bits na direita, pois só estamos interessados no bit mais significativo, em vermelho. Abaixo está a explicação de cada caso:

Caso 1: A soma de dois números positivos gera um negativo. Ocorre Overflow. No caso entra 1 no MSB e 0 no carry.

Caso 2: A soma de dois números negativos gera um positivo. Ocorre Overflow. No caso entra 0 no MSB e 1 no carry.

Caso 3: A soma de dois números positivos gera um positivo. Não ocorre Overflow. No caso entra 0 no MSB e 0 no carry.

Caso 4: A soma de dois números negativos gera um negativo. Não ocorre Overflow. No caso entra 1 no MSB e 1 no carry.

Caso 5: Os dois números tem sinais diferentes. Não ocorre Overflow quando os dois operandos tem dinais diferentes.

Overflow na Subtração

A subtração vou deixar como lição de casa para que vocês criem algum código pra Snes ou Mega que mostre o que acontece com o Overflow na subtração.

Mas vou dar uma breve descrição do que ocorre na subtração.

Temos duas possibilidades:

Realizar a soma com o complemento de 2

A primeira possibilidade é fazer a soma com o complemento de 2 em vez da subtração “real”. Por exemplo, se tivermos a operação “x - y”, podemos realizar essa subtração fazendo “x + complemento2(y)”. Isso gera o mesmo resultado se fizéssemos a subtração real.

Como agora estamos realizando uma soma, as regras são as mesmas que já foram explicadas acima.

Realizar a subtração real

Se formos usar a subtração real, as regras mudam um pouco em relação à soma.

1-) Se os dois operandos tiverem o mesmo sinal, então nunca ocorre overflow.

2-) Se os dois operandos tiverem sinais diferentes, então ocorre overflow nos seguintes casos:

  negativo - positivo = positivo
  positivo - negativo = negativo

Aconselho tentarem entender essas regras. Lembrem que “x - (-y) == x + y”.

Overflow no Shift

Falarei do shift em episódios futuros, porém vou explicar rapidamente.

No caso do shift só temos um operando, então as regras mudam, porém também giram em torno da troca de sinal.

Na Cpu Motorola 68000 temos dois tipos de shift, o lógico e o aritmético. O aritmético é o que trata o número como com sinal e seta a flag de overflow. De acordo com a documentação da Cpu um overflow ocorre se em algum momento durante o shift dos bits ocorrer a troca de sinal. Por exemplo, caso fizermos um shift de 5 para a esquerda, se em algum momento durante o shift um dos 5 bits que sai para o carry trocar o sinal do resultado, a flag overflow é setada, mesmo que o resultado final fique com o mesmo sinal que o do valor inicial.

Portanto é importante verificar na documentação o que cada instrução faz em relação ao overflow.